Theoretical Foundations: Hidden Convexity and Global Optimization
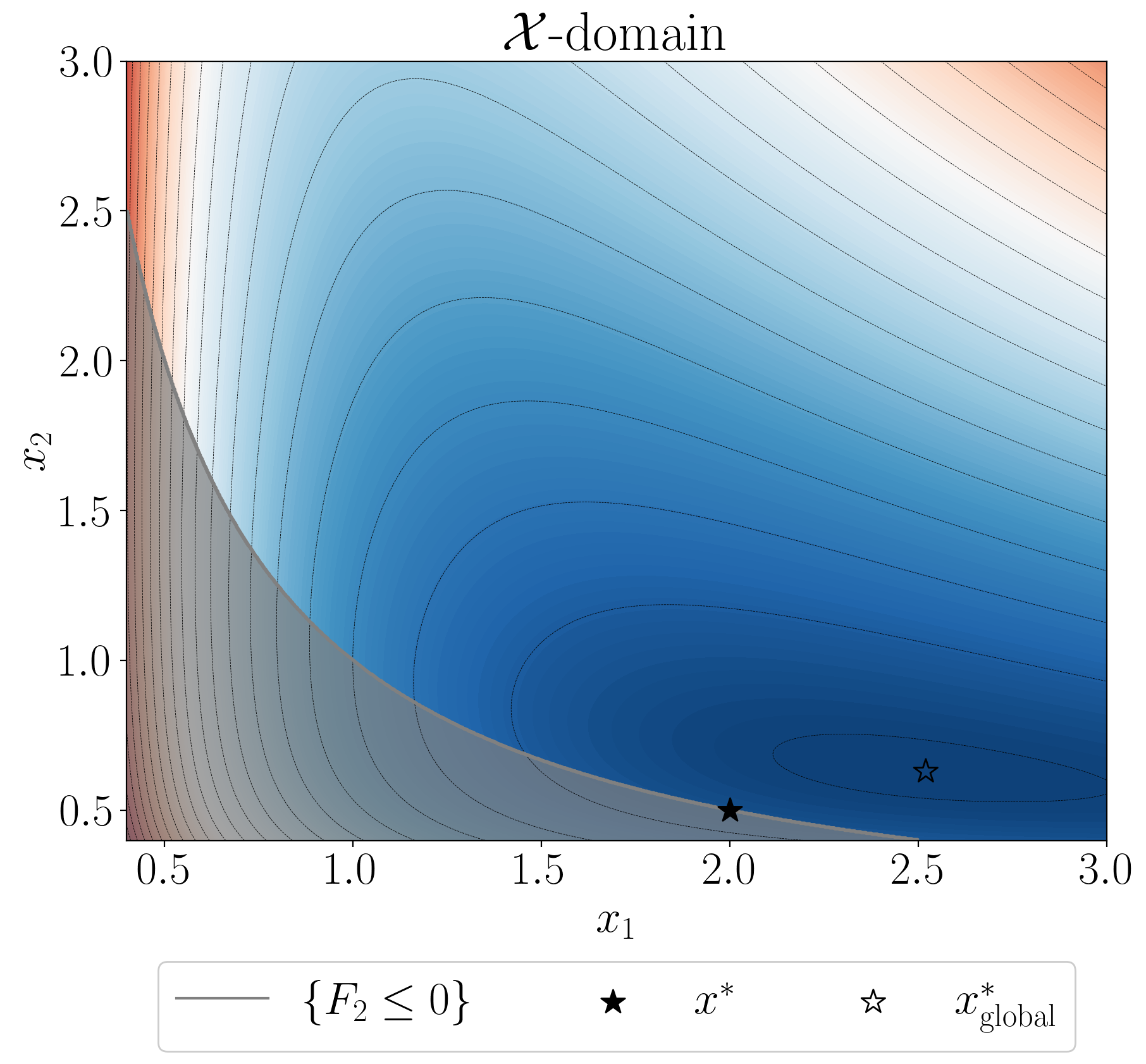
Level sets of objective F1 and the feasible set {F2 ≤ 0} in the original X-domain.

Level sets of reformulated objective H1 and the feasible set {H2 ≤ 0} in the U-domain.
The Challenge: Most practically successful machine learning models involve highly non-convex optimization problems, yet their landscapes remain poorly understood. Traditional optimization theory often fails to explain why gradient methods work so well in practice.
My Approach: I develop the theory of "hidden convexity" — the idea that many seemingly non-convex problems actually admit equivalent convex structures, even if these structures are not directly computable. This framework provides rigorous explanations for the surprising success of optimization methods and enables the design of global solution algorithms.
Key Contributions:
- Analysis of optimization algorithms under hidden convexity (SIAM J. Optim., 2025); helps to resolve open questions in reinforcement learning and variational inference.
- Tackling scenarios with non-convex functional constraints under hidden convexity (NeurIPS COML Workshop, 2025 (Oral)); implies the first global solution method for safe convex reinforcement learning and other applications.
- Global convergence guarantees for natural gradient variational inference in non-conjugate models, using non-Euclidean projections and uncovering the hidden convexity in the variational loss (NeurIPS, 2025).
- Using proporties of hidden convex structure for designing faster policy gradient methods in general utility RL (ICML, 2023).
- Discovering new landscape structures in zero-sum game settings, which allow us improve complexities by orders of magnitude (SIAM J. Contr. Optim., 2025).
- Analyzing the fundamental structures of a linear quadratic regulator with output control. Convergence of carefully designed gradient method (SIAM J. Contr. Optim., 2021).
Impact: This line of work has led to substantial understanding of efficiency of policy gradient methods and provides a principled path for understanding non-convex optimization landscapes in safety-critical applications.
Selected Publications
-
Stochastic Optimization under Hidden Convexity. with N. He, Y. Hu. SIAM Journal on Optimization, 2025.
-
Natural Gradient VI: Guarantees for Non-Conjugate Models. with F. Sun, N. He. NeurIPS, 2025.
-
Global Solutions to Non-Convex Functional Constrained Problems with Hidden Convexity. with N. He, G. Lan, F. Wolf. NeurIPS Workshop COML’25 (Oral). Preprint: arXiv.
-
Learning Zero-Sum Linear Quadratic Games with Improved Sample Complexity and Last-Iterate Convergence. with J. Wu, A. Barakat, N. He. SIAM Journal on Control and Optimization, 2025. Preliminary version in Conference on Decision and Control, 2023.
-
Reinforcement Learning with General Utilities: Simpler Variance Reduction and Large State-Action Space. with A. Barakat, N. He. ICML, 2023.
-
Optimizing Static Linear Feedback: Gradient Method. with B. Polyak. SIAM Journal on Control and Optimization, 2021.
Research Impact
This theoretical framework has enabled breakthrough results in understanding why modern optimization methods work so well in practice, providing the mathematical foundations for reliable AI systems in safety-critical applications.